Hands-on Ex 2

Published

November 19, 2023

Modified

December 16, 2023

1 Part 1

Spatial Weights and Applications

A key aspect of spatial analysis is to measure the strength of the spatial relationships between spatial objects, or how these related spatial objects influence each other. This would allow us to further the analysis by computing spatial autocorrelation indices, implementing spatial econometrics techniques, studying the spatial distribution of observations, as well as performing spatial sampling or graph partitioning. Source: Handbook of Spatial Analysis

Computing spatial weights and neighbor links is a necessary part of this analysis process, and is the key focus of this exercise.

What are Spatial Weights?

Spatial weights are one way to represent graphs in geographic data science and spatial statistics and are widely used to represent geographic relationships between the observational units in a spatial dataset.

  • Spatial weights often express our knowledge about spatial relationships. For example, proximity and adjacency are common spatial questions: What neighborhoods are you surrounded by? How many gas stations are within 5 miles of my stalled car?
  • Spatial questions target specific information about the spatial configuration of a specific target (“a neighborhood,” “my stalled car”) and geographically connected relevant sites (“adjacent neighborhoods”, “nearby gas stations”)

2 Installing R packages

code block 
pacman::p_load(sf, spdep, tmap, tidyverse, knitr, kableExtra, urbnthemes, ggplot2)

3 Scope of Study

Two datasets will be used in this exercise:

  • Geospatial: Hunan county boundary layer set in ESRI shapefile format
  • Aspatial: Hunan’s 2012 local development indicators in csv format

3.1 Loading the data

code block 
hunan <- st_read(dsn = "data/geospatial", 
                 layer = "Hunan")
Reading layer `Hunan' from data source 
  `C:\haileycsy\ISSS624-AGA\Hands-on_Ex\hoe2\data\geospatial' 
  using driver `ESRI Shapefile'
Simple feature collection with 88 features and 7 fields
Geometry type: POLYGON
Dimension:     XY
Bounding box:  xmin: 108.7831 ymin: 24.6342 xmax: 114.2544 ymax: 30.12812
Geodetic CRS:  WGS 84
code block 
hunan2012 <- read_csv("data/aspatial/Hunan_2012.csv")

By performing a left_join(), the geospatial dataframe hunan will be updated with attribute fields of hunan2012

code block 
hunan <- left_join(hunan, hunan2012) %>%
  select(1:4, 7, 15)
code block 
head(hunan,10) %>%
  kbl() %>%
  kable_styling(
    full_width = F, 
    bootstrap_options = c("condensed", "responsive"))
NAME_2 ID_3 NAME_3 ENGTYPE_3 County GDPPC geometry
Changde 21098 Anxiang County Anxiang 23667 POLYGON ((112.0625 29.75523...
Changde 21100 Hanshou County Hanshou 20981 POLYGON ((112.2288 29.11684...
Changde 21101 Jinshi County City Jinshi 34592 POLYGON ((111.8927 29.6013,...
Changde 21102 Li County Li 24473 POLYGON ((111.3731 29.94649...
Changde 21103 Linli County Linli 25554 POLYGON ((111.6324 29.76288...
Changde 21104 Shimen County Shimen 27137 POLYGON ((110.8825 30.11675...
Changsha 21109 Liuyang County City Liuyang 63118 POLYGON ((113.9905 28.5682,...
Changsha 21110 Ningxiang County Ningxiang 62202 POLYGON ((112.7181 28.38299...
Changsha 21111 Wangcheng County Wangcheng 70666 POLYGON ((112.7914 28.52688...
Chenzhou 21112 Anren County Anren 12761 POLYGON ((113.1757 26.82734...

4 Visualising Regional Development Indicators

GDPPC Refers to Gross Domestic Product per capita, which measures a country’s economic output per person. To visualise the distribution of GDPPC as a cloropleth map, qtm() of tmap package can be used.

code block 
# Basemap without GDPPC mapping 
basemap <- tm_shape(hunan) +
  tm_polygons() +
  tm_text("NAME_3", size = .5)

# Cloropleth map
gdppc <- qtm(hunan, "GDPPC")

#Place maps side-by-side
tmap_arrange(basemap, 
             gdppc, 
             asp = 1, 
             ncol = 2)

5 The neighborhood in Spatial Analysis

An important concept in spatial analysis is that of a neighborhood, which refers to those data points that we consider to be proximate to a given focal data point. With area-based vector data (polygons), there are multiple ways to measure proximity:

  • Contiguity-based neighbors consider neighboring polygons to be those that “touch” a focal polygon, and are derived in spdep package with the poly2nb() function

  • Distance-based neighbors are those within a given proximity threshold to a focal polygon; distances are measured between polygon centroid using the knn2nb() function

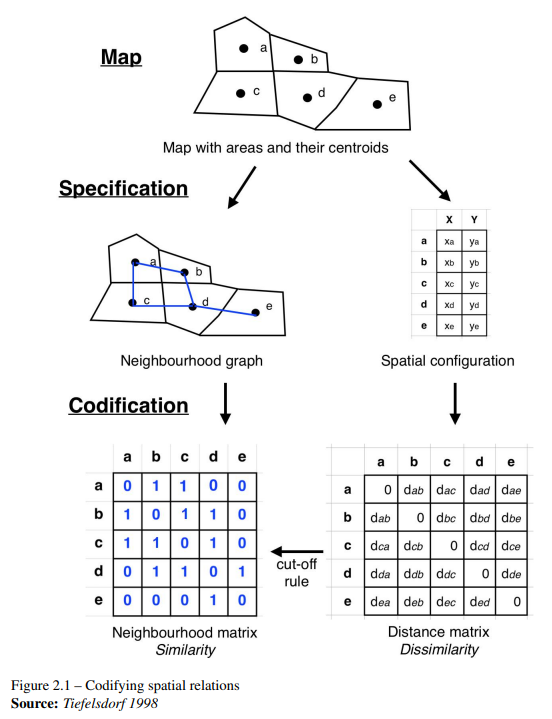
To use this information in statistical analysis, it’s often necessary to compute these relationships between all pairs of observations. This means building a topology —- a mathematical structure that expresses the connectivity between observations —- that we can use to examine the data. A neighborhood matrix is a binary matrix that indicates whether pairs of locations are neighbors or not, expressing this topology of relations with weights 1 and 0.

6 Computing contiguity-based neighbors

Defining a neighbourhood in the sense of contiguity is often used to study demographic and social data, in which it may be more important to be on either side of an administrative boundary than to be located at a certain distance from one another.

Contiguity happens when two spatial units share a common border.

  • Queen Contiguity: A neigboring polygon is one that shares a vertex with the focal polygon
  • Rook Contiguity: A neigboring polygon is one that shares an edge (line segment) with the focal polygon

6.1 Computing Queen contiguity based neighbours

The code chunk below computes a contiguity matrix based on Queen contiguity principle and returns a neighbor list object:

wm_q <- poly2nb(hunan, 
                queen = TRUE)
summary(wm_q)
Neighbour list object:
Number of regions: 88 
Number of nonzero links: 448 
Percentage nonzero weights: 5.785124 
Average number of links: 5.090909 
Link number distribution:

 1  2  3  4  5  6  7  8  9 11 
 2  2 12 16 24 14 11  4  2  1 
2 least connected regions:
30 65 with 1 link
1 most connected region:
85 with 11 links

The summary report shows that:

  • There are 88 area units in Hunan
  • The most connected area unit has 11 neighbors (links)
  • The two least connected areas have only 1 neighbor

For each polygon in our polygon object, wm_q lists all neighboring polygons. For example, to see the neighbors for polygon #1 in the object:

wm_q[[1]]
[1]  2  3  4 57 85

Polygon #1 has 5 neighbors.

We can retrieve the county name of Polygon ID=1 by using the code chunk below:

hunan$County[1]
[1] "Anxiang"

To reveal the county names of the five neighboring polygons, the code chunk will be used:

hunan$NAME_3[c(2,3,4,57,85)]
[1] "Hanshou" "Jinshi"  "Li"      "Nan"     "Taoyuan"
# Store all neighbor polygon IDs in new variable
nb1 <- wm_q[[1]]
# Replace polygon IDs in the variable with respective GDPPC
nb1 <- hunan$GDPPC[nb1]

nb1
[1] 20981 34592 24473 21311 22879

The printed output above shows that the GDPPC of the five nearest neighbors based on Queen’s method are 20981, 34592, 24473, 21311 and 22879 respectively.

6.1.1 Displaying complete matrix

You can display the complete weight matrix by using str()

str(wm_q)
List of 88
 $ : int [1:5] 2 3 4 57 85
 $ : int [1:5] 1 57 58 78 85
 $ : int [1:4] 1 4 5 85
 $ : int [1:4] 1 3 5 6
 $ : int [1:4] 3 4 6 85
 $ : int [1:5] 4 5 69 75 85
 $ : int [1:4] 67 71 74 84
 $ : int [1:7] 9 46 47 56 78 80 86
 $ : int [1:6] 8 66 68 78 84 86
 $ : int [1:8] 16 17 19 20 22 70 72 73
 $ : int [1:3] 14 17 72
 $ : int [1:5] 13 60 61 63 83
 $ : int [1:4] 12 15 60 83
 $ : int [1:3] 11 15 17
 $ : int [1:4] 13 14 17 83
 $ : int [1:5] 10 17 22 72 83
 $ : int [1:7] 10 11 14 15 16 72 83
 $ : int [1:5] 20 22 23 77 83
 $ : int [1:6] 10 20 21 73 74 86
 $ : int [1:7] 10 18 19 21 22 23 82
 $ : int [1:5] 19 20 35 82 86
 $ : int [1:5] 10 16 18 20 83
 $ : int [1:7] 18 20 38 41 77 79 82
 $ : int [1:5] 25 28 31 32 54
 $ : int [1:5] 24 28 31 33 81
 $ : int [1:4] 27 33 42 81
 $ : int [1:3] 26 29 42
 $ : int [1:5] 24 25 33 49 54
 $ : int [1:3] 27 37 42
 $ : int 33
 $ : int [1:8] 24 25 32 36 39 40 56 81
 $ : int [1:8] 24 31 50 54 55 56 75 85
 $ : int [1:5] 25 26 28 30 81
 $ : int [1:3] 36 45 80
 $ : int [1:6] 21 41 47 80 82 86
 $ : int [1:6] 31 34 40 45 56 80
 $ : int [1:4] 29 42 43 44
 $ : int [1:4] 23 44 77 79
 $ : int [1:5] 31 40 42 43 81
 $ : int [1:6] 31 36 39 43 45 79
 $ : int [1:6] 23 35 45 79 80 82
 $ : int [1:7] 26 27 29 37 39 43 81
 $ : int [1:6] 37 39 40 42 44 79
 $ : int [1:4] 37 38 43 79
 $ : int [1:6] 34 36 40 41 79 80
 $ : int [1:3] 8 47 86
 $ : int [1:5] 8 35 46 80 86
 $ : int [1:5] 50 51 52 53 55
 $ : int [1:4] 28 51 52 54
 $ : int [1:5] 32 48 52 54 55
 $ : int [1:3] 48 49 52
 $ : int [1:5] 48 49 50 51 54
 $ : int [1:3] 48 55 75
 $ : int [1:6] 24 28 32 49 50 52
 $ : int [1:5] 32 48 50 53 75
 $ : int [1:7] 8 31 32 36 78 80 85
 $ : int [1:6] 1 2 58 64 76 85
 $ : int [1:5] 2 57 68 76 78
 $ : int [1:4] 60 61 87 88
 $ : int [1:4] 12 13 59 61
 $ : int [1:7] 12 59 60 62 63 77 87
 $ : int [1:3] 61 77 87
 $ : int [1:4] 12 61 77 83
 $ : int [1:2] 57 76
 $ : int 76
 $ : int [1:5] 9 67 68 76 84
 $ : int [1:4] 7 66 76 84
 $ : int [1:5] 9 58 66 76 78
 $ : int [1:3] 6 75 85
 $ : int [1:3] 10 72 73
 $ : int [1:3] 7 73 74
 $ : int [1:5] 10 11 16 17 70
 $ : int [1:5] 10 19 70 71 74
 $ : int [1:6] 7 19 71 73 84 86
 $ : int [1:6] 6 32 53 55 69 85
 $ : int [1:7] 57 58 64 65 66 67 68
 $ : int [1:7] 18 23 38 61 62 63 83
 $ : int [1:7] 2 8 9 56 58 68 85
 $ : int [1:7] 23 38 40 41 43 44 45
 $ : int [1:8] 8 34 35 36 41 45 47 56
 $ : int [1:6] 25 26 31 33 39 42
 $ : int [1:5] 20 21 23 35 41
 $ : int [1:9] 12 13 15 16 17 18 22 63 77
 $ : int [1:6] 7 9 66 67 74 86
 $ : int [1:11] 1 2 3 5 6 32 56 57 69 75 ...
 $ : int [1:9] 8 9 19 21 35 46 47 74 84
 $ : int [1:4] 59 61 62 88
 $ : int [1:2] 59 87
 - attr(*, "class")= chr "nb"
 - attr(*, "region.id")= chr [1:88] "1" "2" "3" "4" ...
 - attr(*, "call")= language poly2nb(pl = hunan, queen = TRUE)
 - attr(*, "type")= chr "queen"
 - attr(*, "sym")= logi TRUE

6.2 Creating Rook contiguity based neighbours

Compute the Rook contiguity matrix by altering queen argument of poly2nb() function to return a neighbor list object:

wm_r <- poly2nb(hunan, 
                queen = FALSE)
summary(wm_r)
Neighbour list object:
Number of regions: 88 
Number of nonzero links: 440 
Percentage nonzero weights: 5.681818 
Average number of links: 5 
Link number distribution:

 1  2  3  4  5  6  7  8  9 10 
 2  2 12 20 21 14 11  3  2  1 
2 least connected regions:
30 65 with 1 link
1 most connected region:
85 with 10 links

The summary report shows that:

  • There are 88 area units in Hunan
  • The most connected area unit has 10 neighbors (links)
  • The two least connected areas have only 1 neighbor

7 Visualising Contiguity 1

A connectivity graph takes a point and displays a line connecting to each neighboring point. The current geospatial dataset only has polygons at the moment, so we will need to compute points in order to make our connectivity graphs. The most typical method for this will be using polygon centroids.

To get our longitude values we map the st_centroid function over the geometry column of us.bound and access the longitude value through double bracket notation [[]] and 1. This allows us to get only the longitude, which is the first value in each centroid.

longitude <- map_dbl(hunan$geometry, ~st_centroid(.x)[[1]])

We do the same for latitude with one key difference. We access the second value per each centroid with [[2]].

latitude <- map_dbl(hunan$geometry, ~st_centroid(.x)[[2]])
coords <- cbind(longitude, latitude)

Check the first few observations to see if things are formatted correctly:

code block 
head(coords)
     longitude latitude
[1,]  112.1531 29.44362
[2,]  112.0372 28.86489
[3,]  111.8917 29.47107
[4,]  111.7031 29.74499
[5,]  111.6138 29.49258
[6,]  111.0341 29.79863

7.1 Plotting Queen contiguity as a map

code block 
plot(hunan$geometry, 
     border = "#ABA9C3")
plot(wm_q, 
     coords, 
     pch = 20, 
     cex = .7, 
     add = TRUE, 
     col= "salmon"
     )

7.2 Plotting Rook contiguity as a map

code block 
plot(hunan$geometry, border="lightgrey")
plot(wm_r, 
     coords, 
     pch = 19, 
     cex = 0.6, 
     add = TRUE, 
     col = "#129490")

7.3 Putting both maps together

code block 
par(mfrow = c(1,2))

# Queen
plot(hunan$geometry, 
     border = "lightgrey")
plot(wm_q, 
     coords, 
     pch = 20, 
     cex = .7, 
     add = TRUE, 
     col = "salmon",
     main = "Queen Contiguity"
     )

# Rook
plot(hunan$geometry, border="lightgrey")
plot(wm_r, 
     coords, 
     pch = 19, 
     cex = 0.6, 
     add = TRUE, 
     col = "#129490",
     main = "Rook Contiguity")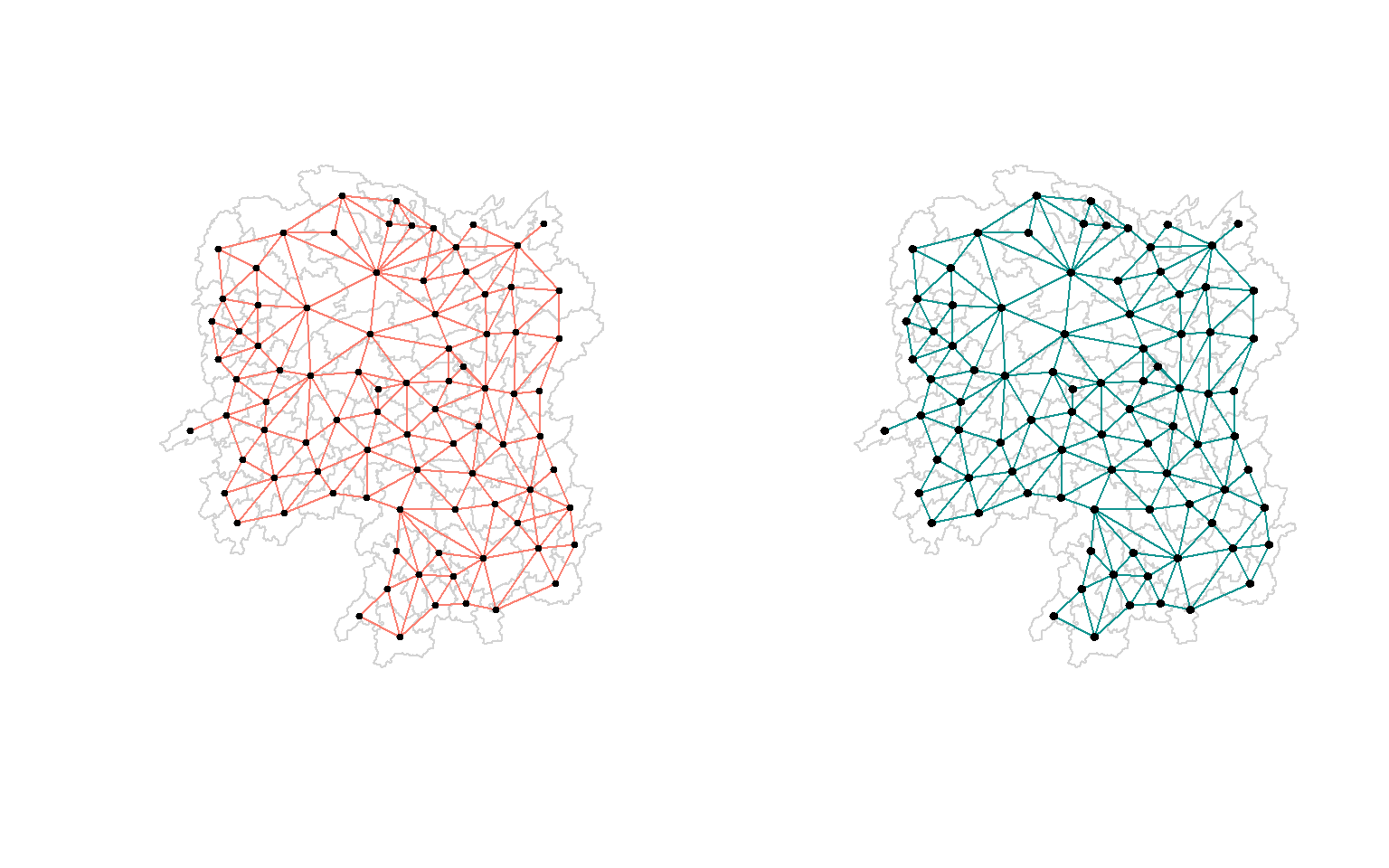

8 Computing distance-based neighbors

Several steps are needed to obtain a distance threshold or cut-off distance that will be used to define neighbors in the analysis. This cut-off distance is crucial for creating a weight matrix that reflects the spatial relationships between regions based on their proximity within this defined distance band.

8.1 Defining cut-off distance

  • knearneigh(coords) is used to find k nearest neighbors for each point in the spatial dataset defined by the coords variable. Returns: k-nearest neighbor object (kn object)

  • knn2nb() is then used to convert the k-nearest neighbor object (kn object) into a neighbors list (nb object). This nb object represents the spatial relationships between neighboring regions based on the k-nearest neighbors and returns a neighbor list object:

k1 <- knn2nb(knearneigh(coords))
k1
Neighbour list object:
Number of regions: 88 
Number of nonzero links: 88 
Percentage nonzero weights: 1.136364 
Average number of links: 1 
25 disjoint connected subgraphs
Non-symmetric neighbours list
  • nbdists() calculates the distances between neighboring regions defined by the neighbors list k1
  • The longlat = TRUE argument indicates that the distances should be calculated assuming longitude and latitude coordinates, and it returns the distances in kilometers
  • unlist() flattens the result, converting it from a list structure to a simple numeric vector
k1dists <- unlist(nbdists(k1, coords, longlat = TRUE))
summary(k1dists)
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
  24.79   32.57   38.01   39.07   44.52   61.79

The summary report shows that the largest first nearest neighbour distance is 61.79 km, so using this as the upper threshold gives certainty that all units will have at least one neighbour.

8.2 Computing fixed distance weight matrix

This is done using dnearneigh():

wm_d62 <- dnearneigh(
  coords, 
  # specify lower and upper distance bands
  0, 62, 
  longlat = TRUE)

wm_d62
Neighbour list object:
Number of regions: 88 
Number of nonzero links: 324 
Percentage nonzero weights: 4.183884 
Average number of links: 3.681818

The summary report shows that:

  • There are 88 area units in Hunan
  • There are 324 links between regions that fall within the distance band of 0 - 62km
  • On average, each region has about 3-4 neighbors that fall within the distance band
str(wm_d62)
List of 88
 $ : int [1:5] 3 4 5 57 64
 $ : int [1:4] 57 58 78 85
 $ : int [1:4] 1 4 5 57
 $ : int [1:3] 1 3 5
 $ : int [1:4] 1 3 4 85
 $ : int 69
 $ : int [1:2] 67 84
 $ : int [1:4] 9 46 47 78
 $ : int [1:4] 8 46 68 84
 $ : int [1:4] 16 22 70 72
 $ : int [1:3] 14 17 72
 $ : int [1:5] 13 60 61 63 83
 $ : int [1:4] 12 15 60 83
 $ : int [1:2] 11 17
 $ : int 13
 $ : int [1:4] 10 17 22 83
 $ : int [1:3] 11 14 16
 $ : int [1:3] 20 22 63
 $ : int [1:5] 20 21 73 74 82
 $ : int [1:5] 18 19 21 22 82
 $ : int [1:6] 19 20 35 74 82 86
 $ : int [1:4] 10 16 18 20
 $ : int [1:3] 41 77 82
 $ : int [1:4] 25 28 31 54
 $ : int [1:4] 24 28 33 81
 $ : int [1:4] 27 33 42 81
 $ : int [1:2] 26 29
 $ : int [1:6] 24 25 33 49 52 54
 $ : int [1:2] 27 37
 $ : int 33
 $ : int [1:2] 24 36
 $ : int 50
 $ : int [1:5] 25 26 28 30 81
 $ : int [1:3] 36 45 80
 $ : int [1:6] 21 41 46 47 80 82
 $ : int [1:5] 31 34 45 56 80
 $ : int [1:2] 29 42
 $ : int [1:3] 44 77 79
 $ : int [1:4] 40 42 43 81
 $ : int [1:3] 39 45 79
 $ : int [1:5] 23 35 45 79 82
 $ : int [1:5] 26 37 39 43 81
 $ : int [1:3] 39 42 44
 $ : int [1:2] 38 43
 $ : int [1:6] 34 36 40 41 79 80
 $ : int [1:5] 8 9 35 47 86
 $ : int [1:5] 8 35 46 80 86
 $ : int [1:5] 50 51 52 53 55
 $ : int [1:4] 28 51 52 54
 $ : int [1:6] 32 48 51 52 54 55
 $ : int [1:4] 48 49 50 52
 $ : int [1:6] 28 48 49 50 51 54
 $ : int [1:2] 48 55
 $ : int [1:5] 24 28 49 50 52
 $ : int [1:4] 48 50 53 75
 $ : int 36
 $ : int [1:5] 1 2 3 58 64
 $ : int [1:5] 2 57 64 66 68
 $ : int [1:3] 60 87 88
 $ : int [1:4] 12 13 59 61
 $ : int [1:5] 12 60 62 63 87
 $ : int [1:4] 61 63 77 87
 $ : int [1:5] 12 18 61 62 83
 $ : int [1:4] 1 57 58 76
 $ : int 76
 $ : int [1:5] 58 67 68 76 84
 $ : int [1:2] 7 66
 $ : int [1:4] 9 58 66 84
 $ : int [1:2] 6 75
 $ : int [1:3] 10 72 73
 $ : int [1:2] 73 74
 $ : int [1:3] 10 11 70
 $ : int [1:4] 19 70 71 74
 $ : int [1:5] 19 21 71 73 86
 $ : int [1:2] 55 69
 $ : int [1:3] 64 65 66
 $ : int [1:3] 23 38 62
 $ : int [1:2] 2 8
 $ : int [1:4] 38 40 41 45
 $ : int [1:5] 34 35 36 45 47
 $ : int [1:5] 25 26 33 39 42
 $ : int [1:6] 19 20 21 23 35 41
 $ : int [1:4] 12 13 16 63
 $ : int [1:4] 7 9 66 68
 $ : int [1:2] 2 5
 $ : int [1:4] 21 46 47 74
 $ : int [1:4] 59 61 62 88
 $ : int [1:2] 59 87
 - attr(*, "class")= chr "nb"
 - attr(*, "region.id")= chr [1:88] "1" "2" "3" "4" ...
 - attr(*, "call")= language dnearneigh(x = coords, d1 = 0, d2 = 62, longlat = TRUE)
 - attr(*, "dnn")= num [1:2] 0 62
 - attr(*, "bounds")= chr [1:2] "GE" "LE"
 - attr(*, "nbtype")= chr "distance"
 - attr(*, "sym")= logi TRUE

Use a combination oftable() and card() to return a contingency matrix of number of neighbors per country:

table(hunan$County, 
    # list number of neighbors for each area
      card(wm_d62))
               
                1 2 3 4 5 6
  Anhua         1 0 0 0 0 0
  Anren         0 0 0 1 0 0
  Anxiang       0 0 0 0 1 0
  Baojing       0 0 0 0 1 0
  Chaling       0 0 1 0 0 0
  Changning     0 0 1 0 0 0
  Changsha      0 0 0 1 0 0
  Chengbu       0 1 0 0 0 0
  Chenxi        0 0 0 1 0 0
  Cili          0 1 0 0 0 0
  Dao           0 0 0 1 0 0
  Dongan        0 0 1 0 0 0
  Dongkou       0 0 0 1 0 0
  Fenghuang     0 0 0 1 0 0
  Guidong       0 0 1 0 0 0
  Guiyang       0 0 0 1 0 0
  Guzhang       0 0 0 0 0 1
  Hanshou       0 0 0 1 0 0
  Hengdong      0 0 0 0 1 0
  Hengnan       0 0 0 0 1 0
  Hengshan      0 0 0 0 0 1
  Hengyang      0 0 0 0 0 1
  Hongjiang     0 0 0 0 1 0
  Huarong       0 0 0 1 0 0
  Huayuan       0 0 0 1 0 0
  Huitong       0 0 0 1 0 0
  Jiahe         0 0 0 0 1 0
  Jianghua      0 0 1 0 0 0
  Jiangyong     0 1 0 0 0 0
  Jingzhou      0 1 0 0 0 0
  Jinshi        0 0 0 1 0 0
  Jishou        0 0 0 0 0 1
  Lanshan       0 0 0 1 0 0
  Leiyang       0 0 0 1 0 0
  Lengshuijiang 0 0 1 0 0 0
  Li            0 0 1 0 0 0
  Lianyuan      0 0 0 0 1 0
  Liling        0 1 0 0 0 0
  Linli         0 0 0 1 0 0
  Linwu         0 0 0 1 0 0
  Linxiang      1 0 0 0 0 0
  Liuyang       0 1 0 0 0 0
  Longhui       0 0 1 0 0 0
  Longshan      0 1 0 0 0 0
  Luxi          0 0 0 0 1 0
  Mayang        0 0 0 0 0 1
  Miluo         0 0 0 0 1 0
  Nan           0 0 0 0 1 0
  Ningxiang     0 0 0 1 0 0
  Ningyuan      0 0 0 0 1 0
  Pingjiang     0 1 0 0 0 0
  Qidong        0 0 1 0 0 0
  Qiyang        0 0 1 0 0 0
  Rucheng       0 1 0 0 0 0
  Sangzhi       0 1 0 0 0 0
  Shaodong      0 0 0 0 1 0
  Shaoshan      0 0 0 0 1 0
  Shaoyang      0 0 0 1 0 0
  Shimen        1 0 0 0 0 0
  Shuangfeng    0 0 0 0 0 1
  Shuangpai     0 0 0 1 0 0
  Suining       0 0 0 0 1 0
  Taojiang      0 1 0 0 0 0
  Taoyuan       0 1 0 0 0 0
  Tongdao       0 1 0 0 0 0
  Wangcheng     0 0 0 1 0 0
  Wugang        0 0 1 0 0 0
  Xiangtan      0 0 0 1 0 0
  Xiangxiang    0 0 0 0 1 0
  Xiangyin      0 0 0 1 0 0
  Xinhua        0 0 0 0 1 0
  Xinhuang      1 0 0 0 0 0
  Xinning       0 1 0 0 0 0
  Xinshao       0 0 0 0 0 1
  Xintian       0 0 0 0 1 0
  Xupu          0 1 0 0 0 0
  Yanling       0 0 1 0 0 0
  Yizhang       1 0 0 0 0 0
  Yongshun      0 0 0 1 0 0
  Yongxing      0 0 0 1 0 0
  You           0 0 0 1 0 0
  Yuanjiang     0 0 0 0 1 0
  Yuanling      1 0 0 0 0 0
  Yueyang       0 0 1 0 0 0
  Zhijiang      0 0 0 0 1 0
  Zhongfang     0 0 0 1 0 0
  Zhuzhou       0 0 0 0 1 0
  Zixing        0 0 1 0 0 0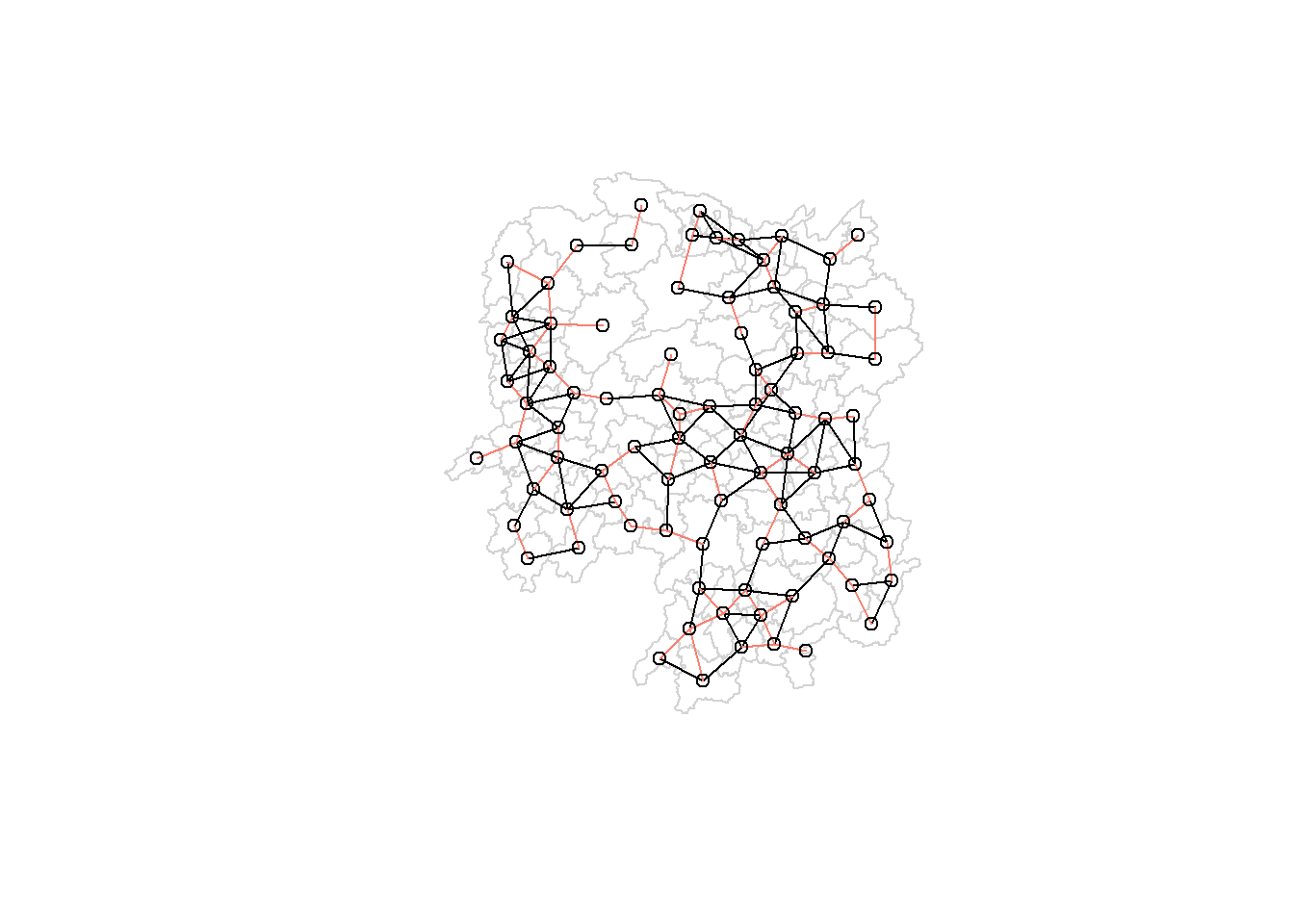

9 Visualising Contiguity 2

code block 
plot(hunan$geometry, border = "lightgrey")

plot(wm_d62, coords, add = TRUE)
plot(k1, coords, add = TRUE, col = "salmon", length = .08)

The red lines show the links of 1st nearest neighbours and the black lines show the links of neighbors within the cut-off distance of 62km.

code block 
par(mfrow=c(1,2))
par(family = "mono")

plot(hunan$geometry, border="lightgrey")

plot(k1, coords, add=TRUE, col="salmon", length=0.08, main="1st nearest neighbours")
title("1st Nearest Neighbours")

plot(hunan$geometry, border="lightgrey")

plot(wm_d62, coords, add=TRUE, pch = 19, cex = 0.6, main="Distance links")
title("Distance Links")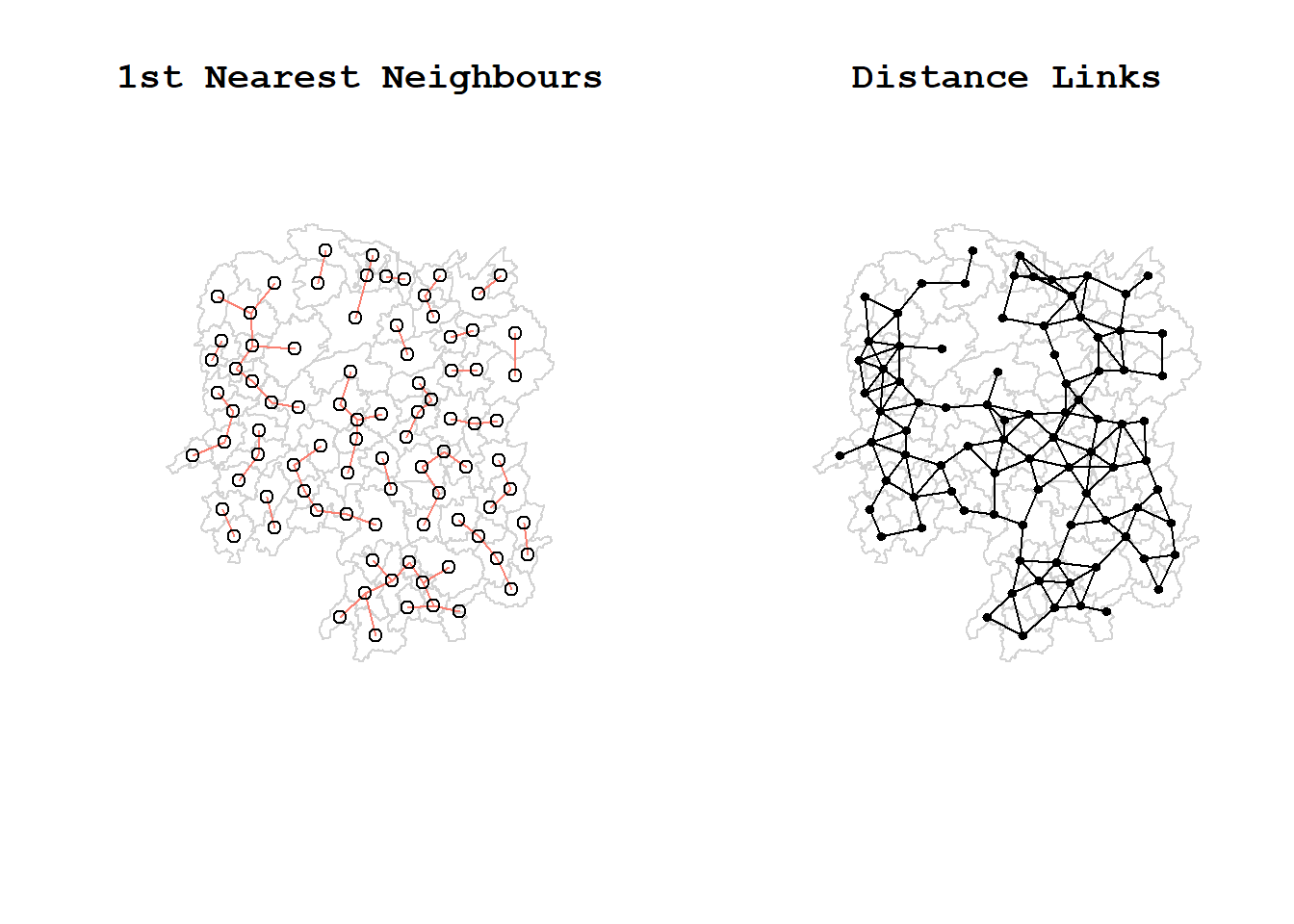

10 Computing Adaptive distance weight matrix

In fixed distance weight matrices, more densely populated areas (usually the urban areas) tend to have more neighbors and the less densely settled areas (usually the rural counties) tend to have fewer neighbors. Having many neighbors smoothes the neighbor relationship across more neighbors.

It is possible to control the numbers of neighbors directly using k-nearest neighbors, either accepting asymmetric neighbors or imposing symmetry – stating k = n as a parameter where n = number of neighbors:

knn6 <- knn2nb(knearneigh(coords, k = 6))
knn6
Neighbour list object:
Number of regions: 88 
Number of nonzero links: 528 
Percentage nonzero weights: 6.818182 
Average number of links: 6 
Non-symmetric neighbours list
code block 
plot(hunan$geometry, border="#dfdfeb")

plot(knn6, 
     coords, 
     pch = 15, 
     cex = .6, 
     add = TRUE, 
     col = "#7F0799")

11 Computing Inversed Distance Weights (IDW)

The Inverse Distance method assigns weights to neighboring locations based on the inverse of the distance between them. The closer two locations are, the higher the weight assigned to their relationship. In an IDW spatial weight matrix, regions that are closer to each other will have higher weights, indicating a stronger spatial relationship.

The following steps are taken to calculate the inverse of distances for each pair of neighboring regions based on a given spatial weight matrix wm_q and the corresponding spatial coordinates, coords.

This is done through nbdists() of spdep:

code block 
# Calculate distance between points
dist <- nbdists(wm_q, coords, longlat = TRUE)

# Calculate the inverse distance of each element in dist
ids <- lapply(dist, function(x) 1/(x))
head(ids)
[[1]]
[1] 0.01535405 0.03916350 0.01820896 0.02807922 0.01145113

[[2]]
[1] 0.01535405 0.01764308 0.01925924 0.02323898 0.01719350

[[3]]
[1] 0.03916350 0.02822040 0.03695795 0.01395765

[[4]]
[1] 0.01820896 0.02822040 0.03414741 0.01539065

[[5]]
[1] 0.03695795 0.03414741 0.01524598 0.01618354

[[6]]
[1] 0.015390649 0.015245977 0.021748129 0.011883901 0.009810297

12 Weight Matrix Standardisation

The sum of the weights of the neighbors of a zone is called its degree of connection. Standardized matrices ensure that the degree of connection will depend on the number of its neighbours, which creates heterogeneity between the zones.

Types of Standardization:

  • Row Standardization, “W”
  • Global Standardization, “C”
  • Uniform Standardization, “U”
  • Variance Stabilization, “S”
  • No Standardization, “B”

In general, Row standardization gives more weight to observations bordering the study zone, with a small number of neighbors. In global or uniform standardization, the observations in the centre of the study zone with a large number of neighbors, and are thus subject to more external influences than the border zones. This heterogeneity can have a significant impact on the results of spatial autocorrelation tests.

12.1 Row Standardization

Row-standardization involves dividing each weight in a row by the sum of weights in that row. This ensures that the weights for each observation (row) in the matrix sum to 1, making it a row-standardized spatial weight matrix.

Row-standardization helps to remove the influence of the number of neighbors each observation has, making the spatial weight matrix more comparable across different datasets or regions.

nb2listw() function converts a neighbors list object into a weight list object:

rswm_q <- nb2listw(wm_q, 
            # Specify spatial weights matrix
                   style = "W", 
            # regions with no neighbors are retained in matrix, weights set to zero
                   zero.policy = TRUE)
rswm_q
Characteristics of weights list object:
Neighbour list object:
Number of regions: 88 
Number of nonzero links: 448 
Percentage nonzero weights: 5.785124 
Average number of links: 5.090909 

Weights style: W 
Weights constants summary:
   n   nn S0       S1       S2
W 88 7744 88 37.86334 365.9147
code block 
summary(unlist(rswm_q$weights))
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
0.09091 0.14286 0.20000 0.19643 0.20000 1.00000

12.2 Unstandardized weight matrix

style = “B” Creates a binary (unstandardized) weight list object:

code block 
rswm_ids <- nb2listw(wm_q, glist = ids, style = "B", zero.policy = TRUE)
rswm_ids
Characteristics of weights list object:
Neighbour list object:
Number of regions: 88 
Number of nonzero links: 448 
Percentage nonzero weights: 5.785124 
Average number of links: 5.090909 

Weights style: B 
Weights constants summary:
   n   nn       S0        S1     S2
B 88 7744 8.786867 0.3776535 3.8137
code block 
summary(unlist(rswm_ids$weights))
    Min.  1st Qu.   Median     Mean  3rd Qu.     Max. 
0.008218 0.015088 0.018739 0.019614 0.022823 0.040338

13 Spatial lag variables

Spatial lag variables are used to account for spatial autocorrelation in the data, where the values of a variables in one location are influenced by the values of the variable in nearby locations. A spatially lagged variable is a weighted sum or a weighted average of the neighboring values for that variable where Lag = E(x) or average value of the neighborhood

Creating different spatially lagged variables:

  • spatial lag with row-standardized weights
  • spatial lag as a sum of neighboring values
  • spatial window average
  • spatial window sum

13.1 Spatial lag with row-standardized weights

The following code calculates the GDPPC Lag value, or average neighbor GDPPC value for each polygon and returns it as a numeric vector:

GDPPC_lag <- lag.listw(rswm_q, hunan$GDPPC)
GDPPC_lag 
 [1] 24847.20 22724.80 24143.25 27737.50 27270.25 21248.80 43747.00 33582.71
 [9] 45651.17 32027.62 32671.00 20810.00 25711.50 30672.33 33457.75 31689.20
[17] 20269.00 23901.60 25126.17 21903.43 22718.60 25918.80 20307.00 20023.80
[25] 16576.80 18667.00 14394.67 19848.80 15516.33 20518.00 17572.00 15200.12
[33] 18413.80 14419.33 24094.50 22019.83 12923.50 14756.00 13869.80 12296.67
[41] 15775.17 14382.86 11566.33 13199.50 23412.00 39541.00 36186.60 16559.60
[49] 20772.50 19471.20 19827.33 15466.80 12925.67 18577.17 14943.00 24913.00
[57] 25093.00 24428.80 17003.00 21143.75 20435.00 17131.33 24569.75 23835.50
[65] 26360.00 47383.40 55157.75 37058.00 21546.67 23348.67 42323.67 28938.60
[73] 25880.80 47345.67 18711.33 29087.29 20748.29 35933.71 15439.71 29787.50
[81] 18145.00 21617.00 29203.89 41363.67 22259.09 44939.56 16902.00 16930.00
# create a list of Hunan provinces and corresponding spatial lag GDPPC values
lag_list <- list(hunan$NAME_3, lag.listw(rswm_q, hunan$GDPPC))

# Transform list into dataframe
lag_res <- as.data.frame(lag_list)

# Assign column names to dataframe
colnames(lag_res) <- c("NAME_3", "lag GDPPC")

# Join to main hunan dataframe
hunan <- left_join(hunan,lag_res)

head(hunan)
Simple feature collection with 6 features and 7 fields
Geometry type: POLYGON
Dimension:     XY
Bounding box:  xmin: 110.4922 ymin: 28.61762 xmax: 112.3013 ymax: 30.12812
Geodetic CRS:  WGS 84
   NAME_2  ID_3  NAME_3   ENGTYPE_3  County GDPPC lag GDPPC
1 Changde 21098 Anxiang      County Anxiang 23667  24847.20
2 Changde 21100 Hanshou      County Hanshou 20981  22724.80
3 Changde 21101  Jinshi County City  Jinshi 34592  24143.25
4 Changde 21102      Li      County      Li 24473  27737.50
5 Changde 21103   Linli      County   Linli 25554  27270.25
6 Changde 21104  Shimen      County  Shimen 27137  21248.80
                        geometry
1 POLYGON ((112.0625 29.75523...
2 POLYGON ((112.2288 29.11684...
3 POLYGON ((111.8927 29.6013,...
4 POLYGON ((111.3731 29.94649...
5 POLYGON ((111.6324 29.76288...
6 POLYGON ((110.8825 30.11675...

This reveals that lag GDPPC is stored as a new column in the hunan dataframe.

Comparing GDPPC and Spatial Lag GDPPC

code block 
# Plot normal GDPPC cloropleth map
gdppc <- qtm(hunan, "GDPPC")

# Plot lag GDPPC cloropleth map
lag_gdppc <- qtm(hunan, "lag GDPPC")

# Arrange in 2 columns
tmap_arrange(gdppc, lag_gdppc, asp = 1, ncol = 2)

13.2 Spatial lag as a sum of neighboring values

Another way to calculate spatial lag is to sum neighboring values by assigning binary weights.

13.3 Create binary spatial weights matrix

code block 
# For every neighbor an area has, assign value '1'
b_weights <- lapply(wm_q, function(x) 0*x +1)

# Create binary spatial weight matrix
b_weights2 <- nb2listw(wm_q, 
                       glist = b_weights, 
                       style = "B")

b_weights2
Characteristics of weights list object:
Neighbour list object:
Number of regions: 88 
Number of nonzero links: 448 
Percentage nonzero weights: 5.785124 
Average number of links: 5.090909 

Weights style: B 
Weights constants summary:
   n   nn  S0  S1    S2
B 88 7744 448 896 10224

13.4 Compute Lag GDPPC

# create a list of Hunan provinces and corresponding spatial lag GDPPC values
lag_sum <- list(hunan$NAME_3, lag.listw(b_weights2, hunan$GDPPC))

# Transform list object into dataframe
lag_res <- as.data.frame(lag_sum)

# assign column names
colnames(lag_res) <- c("NAME_3", "lag_sum GDPPC")

# Append to hunan dataframe

hunan <- left_join(hunan, lag_res)

Comparing GDPPC and Spatial Lag GDPPC

code block 
# original GDPPC Plot
gdppc <- qtm(hunan, "GDPPC")

# Lag sum GDPPC plot
lag_sum_gdppc <- qtm(hunan, "lag_sum GDPPC")

# Arrange side by side
tmap_arrange(gdppc, lag_sum_gdppc, asp=1, ncol=2)

13.5 Spatial window average

The spatial window average uses row-standardized weights and includes the diagonal element. To do this in R, we need to go back to the neighbors structure and add the diagonal element before assigning weights.

Using the include.self() method from spdep package modifies the existing spatial weights matrix such that each spatial unit is considered a neighbor to itself. Below is the neighbot list for polygon #1, which now has 6 neighbors instead of the original 5:

code block 
wm_qs <- include.self(wm_q)
wm_qs[[1]]
[1]  1  2  3  4 57 85
code block 
wm_qs <- nb2listw(wm_qs)
wm_qs
Characteristics of weights list object:
Neighbour list object:
Number of regions: 88 
Number of nonzero links: 536 
Percentage nonzero weights: 6.921488 
Average number of links: 6.090909 

Weights style: W 
Weights constants summary:
   n   nn S0       S1       S2
W 88 7744 88 30.90265 357.5308
code block 
lag_w_avg_gpdpc <- lag.listw(wm_qs, 
                             hunan$GDPPC)
lag_w_avg_gpdpc
 [1] 24650.50 22434.17 26233.00 27084.60 26927.00 22230.17 47621.20 37160.12
 [9] 49224.71 29886.89 26627.50 22690.17 25366.40 25825.75 30329.00 32682.83
[17] 25948.62 23987.67 25463.14 21904.38 23127.50 25949.83 20018.75 19524.17
[25] 18955.00 17800.40 15883.00 18831.33 14832.50 17965.00 17159.89 16199.44
[33] 18764.50 26878.75 23188.86 20788.14 12365.20 15985.00 13764.83 11907.43
[41] 17128.14 14593.62 11644.29 12706.00 21712.29 43548.25 35049.00 16226.83
[49] 19294.40 18156.00 19954.75 18145.17 12132.75 18419.29 14050.83 23619.75
[57] 24552.71 24733.67 16762.60 20932.60 19467.75 18334.00 22541.00 26028.00
[65] 29128.50 46569.00 47576.60 36545.50 20838.50 22531.00 42115.50 27619.00
[73] 27611.33 44523.29 18127.43 28746.38 20734.50 33880.62 14716.38 28516.22
[81] 18086.14 21244.50 29568.80 48119.71 22310.75 43151.60 17133.40 17009.33
# create a list of Hunan provinces and corresponding spatial lag GDPPC values
lag.list.wm_qs <- list(hunan$NAME_3, lag.listw(wm_qs, hunan$GDPPC))

# Transform list object into dataframe
lag_wm_qs.res <- as.data.frame(lag.list.wm_qs)

# Assign column names
colnames(lag_wm_qs.res) <- c("NAME_3", "lag_window_avg GDPPC")

# Add to main dataframe
hunan <- left_join(hunan, lag_wm_qs.res)
code block 
head(hunan,10) %>%
  kbl() %>%
  kable_styling(
    full_width = F, 
    bootstrap_options = c("condensed", "responsive"))
NAME_2 ID_3 NAME_3 ENGTYPE_3 County GDPPC lag GDPPC lag_sum GDPPC lag_window_avg GDPPC geometry
Changde 21098 Anxiang County Anxiang 23667 24847.20 124236 24650.50 POLYGON ((112.0625 29.75523...
Changde 21100 Hanshou County Hanshou 20981 22724.80 113624 22434.17 POLYGON ((112.2288 29.11684...
Changde 21101 Jinshi County City Jinshi 34592 24143.25 96573 26233.00 POLYGON ((111.8927 29.6013,...
Changde 21102 Li County Li 24473 27737.50 110950 27084.60 POLYGON ((111.3731 29.94649...
Changde 21103 Linli County Linli 25554 27270.25 109081 26927.00 POLYGON ((111.6324 29.76288...
Changde 21104 Shimen County Shimen 27137 21248.80 106244 22230.17 POLYGON ((110.8825 30.11675...
Changsha 21109 Liuyang County City Liuyang 63118 43747.00 174988 47621.20 POLYGON ((113.9905 28.5682,...
Changsha 21110 Ningxiang County Ningxiang 62202 33582.71 235079 37160.12 POLYGON ((112.7181 28.38299...
Changsha 21111 Wangcheng County Wangcheng 70666 45651.17 273907 49224.71 POLYGON ((112.7914 28.52688...
Chenzhou 21112 Anren County Anren 12761 32027.62 256221 29886.89 POLYGON ((113.1757 26.82734...

Comparing lag GDPPC to window average Lag GDPPC

code block 
w_avg_gdppc <- qtm(hunan, "lag_window_avg GDPPC")
tmap_arrange(lag_gdppc, w_avg_gdppc, asp=1, ncol=2)

13.6 Spatial window sum

This is similar to the spatial window average, but without using row-standardized weights.

Polygon #1 now has 6 neighbors instead of 5:

wm_qs <- include.self(wm_q)
b_weights <- lapply(wm_qs, function(x) 0*x + 1)
b_weights[1]
[[1]]
[1] 1 1 1 1 1 1
# Assign weights values
b_weights2 <- nb2listw(wm_qs, 
                       glist = b_weights, 
                       style = "B")
b_weights2
Characteristics of weights list object:
Neighbour list object:
Number of regions: 88 
Number of nonzero links: 536 
Percentage nonzero weights: 6.921488 
Average number of links: 6.090909 

Weights style: B 
Weights constants summary:
   n   nn  S0   S1    S2
B 88 7744 536 1072 14160
code block 
# Compute lag value
w_sum_gdppc <- list(hunan$NAME_3, lag.listw(b_weights2, hunan$GDPPC))

w_sum_gdppc.res <- as.data.frame(w_sum_gdppc)

colnames(w_sum_gdppc.res) <- c("NAME_3", "w_sum GDPPC")

hunan <- left_join(hunan, w_sum_gdppc.res)
code block 
head(hunan,10) %>%
  kbl() %>%
  kable_styling(
    full_width = F, 
    bootstrap_options = c("condensed", "responsive"))
NAME_2 ID_3 NAME_3 ENGTYPE_3 County GDPPC lag GDPPC lag_sum GDPPC lag_window_avg GDPPC w_sum GDPPC geometry
Changde 21098 Anxiang County Anxiang 23667 24847.20 124236 24650.50 147903 POLYGON ((112.0625 29.75523...
Changde 21100 Hanshou County Hanshou 20981 22724.80 113624 22434.17 134605 POLYGON ((112.2288 29.11684...
Changde 21101 Jinshi County City Jinshi 34592 24143.25 96573 26233.00 131165 POLYGON ((111.8927 29.6013,...
Changde 21102 Li County Li 24473 27737.50 110950 27084.60 135423 POLYGON ((111.3731 29.94649...
Changde 21103 Linli County Linli 25554 27270.25 109081 26927.00 134635 POLYGON ((111.6324 29.76288...
Changde 21104 Shimen County Shimen 27137 21248.80 106244 22230.17 133381 POLYGON ((110.8825 30.11675...
Changsha 21109 Liuyang County City Liuyang 63118 43747.00 174988 47621.20 238106 POLYGON ((113.9905 28.5682,...
Changsha 21110 Ningxiang County Ningxiang 62202 33582.71 235079 37160.12 297281 POLYGON ((112.7181 28.38299...
Changsha 21111 Wangcheng County Wangcheng 70666 45651.17 273907 49224.71 344573 POLYGON ((112.7914 28.52688...
Chenzhou 21112 Anren County Anren 12761 32027.62 256221 29886.89 268982 POLYGON ((113.1757 26.82734...

Comparing all the plots

code block 
w_sum_gdppc <- qtm(hunan, "w_sum GDPPC")
tmap_arrange(gdppc, lag_gdppc, lag_sum_gdppc, w_avg_gdppc, w_sum_gdppc, 
             nrow = 2, asp = 1)

14 Part 2

Global and Local Measures of Autocorrelation (GLISA)

One of the key questions for Geospatial Analysis is to uncover the geographical distribution of values across spatial areas. Given a set of areal features and an associated variable,

  • global statistical tools evaluate whether the distribution of that variable follows a clustered, dispersed or random pattern
  • local indicators evaluate the existence of clusters in the spatial arrangement of that variable

15 Global Measures of Spatial Autocorrelation

15.1 Global Moran’s I

Excerpt from ArcGIS Pro

The tool conducts the following calculations to derive an Index Value, Expected Index value, z-score and p-value:

  1. Compute the mean (\(\mu\)) and variance (\(\sigma\)) for the variable being evaluated
  2. For each feature value x, derive the deviation from the mean (d) where \(d = x - \mu\)
  3. Deviation values d of all neighboring areas are multiplied together to create a cross-product, P

If the values in the dataset tend to cluster spatially (high values cluster near other high values; low values cluster near other low values), the Moran’s Index will be positive. When high values repel other high values, and tend to be near low values, the Index will be negative. If positive cross-product values balance negative cross-product values, the Index will tend towards zero.

Given the number of features in the dataset and the variance for the data values overall, the tool computes a z-score and p-value indicating whether this difference is statistically significant or not. Index values cannot be interpreted directly; they can only be interpreted within the context of the null hypothesis.

As an inferential statistic, Global Moran’s I tests the following hypothesis:

\[H_0: \text{The variable is randomly distributed among the spatial features in the study area}\] \[H_1: \text{The variable is not randomly distributed among the spatial features in the study area}\] Interpretation of statistical significance & distribution:

+ve Moran’s I -ve Moran’s I
p-value < 0.05
(significant)		 Reject \(H_0\)
Variable is Spatially Clustered		 Reject \(H_0\)
Variable is Spatially Dispersed
p-value > 0.05
(Not significant)		 Accept \(H_0\)
Variable is randomly distributed

The code chunk below performs Moran’s I statistical testing using moran.test() of spdep:

moran.test(hunan$GDPPC, 
           listw = rswm_q, 
           zero.policy = TRUE, 
           na.action = na.omit)

    Moran I test under randomisation

data:  hunan$GDPPC  
weights: rswm_q    

Moran I statistic standard deviate = 4.7351, p-value = 1.095e-06
alternative hypothesis: greater
sample estimates:
Moran I statistic       Expectation          Variance 
      0.300749970      -0.011494253       0.004348351

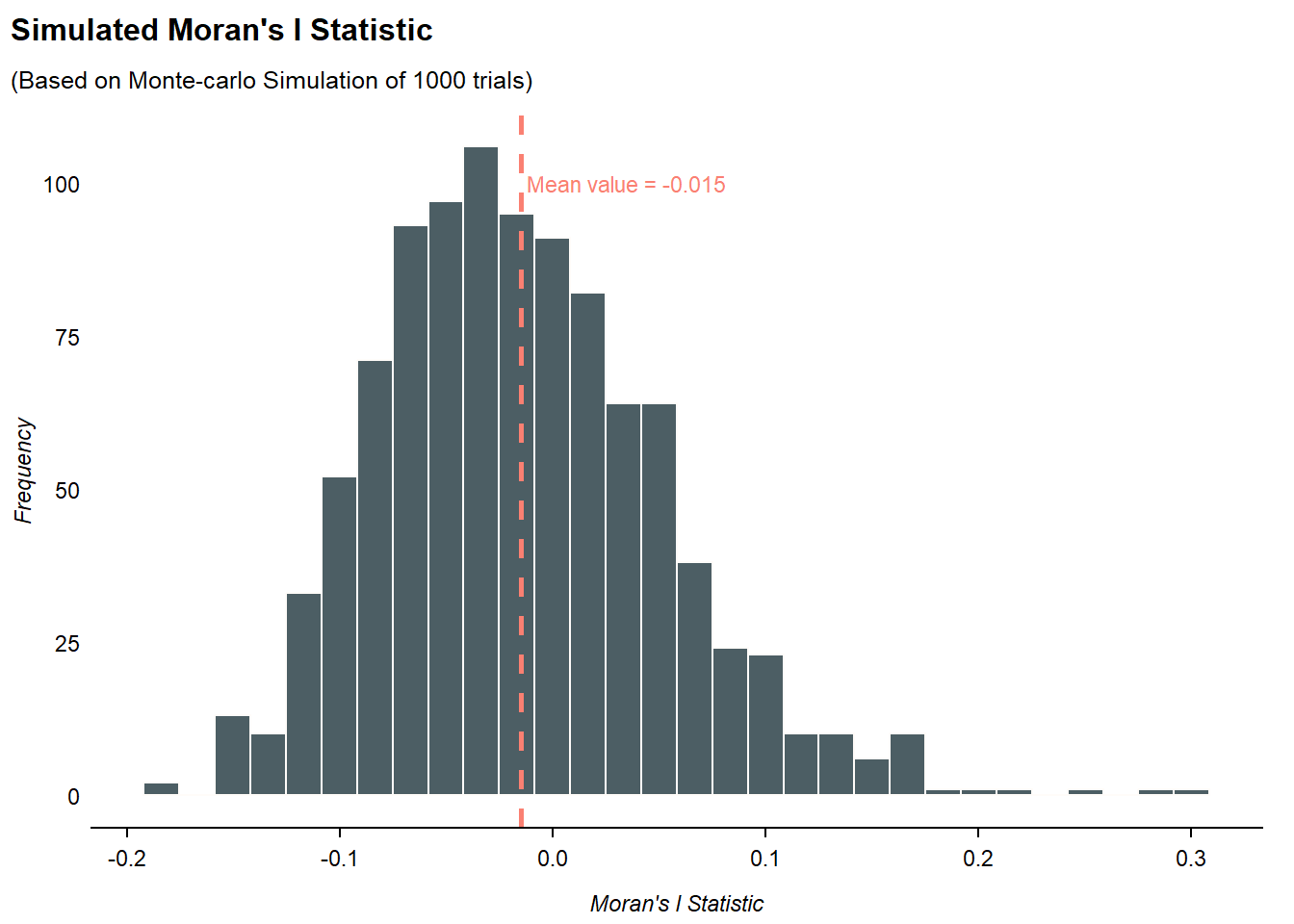
From the test results, p-value is < 0.05, so we reject \(H_0\) and conclude that the variable is not randomly distributed among the spatial features in the study area. The alternative hypothesis: greater indicates a positive spatial autocorrelation, suggestive of spatial clustering.

The code chunk below performs a Monte Carlo simulation of n= 1000 trials for Moran’s I statistic by using moran.mc() of spdep:

set.seed(1234)

bperm <- moran.mc(hunan$GDPPC, 
                listw = rswm_q, 
                nsim = 999, 
                zero.policy = TRUE, 
                na.action = na.omit)
bperm

    Monte-Carlo simulation of Moran I

data:  hunan$GDPPC 
weights: rswm_q  
number of simulations + 1: 1000 

statistic = 0.30075, observed rank = 1000, p-value = 0.001
alternative hypothesis: greater

From the Monte Crlo simulation test results, p-value is < 0.05, so we reject \(H_0\) and conclude that the variable is not randomly distributed among the spatial features in the study area. The alternative hypothesis: greater indicates a positive spatial autocorrelation, suggestive of spatial clustering.

15.1.1 Visualising the results of Monte Carlo Moran’s I Test

code block 
# Extract result
sim_moran <- bperm$res
# Calculate mean result
sim_mean <- mean(sim_moran)

set_urbn_defaults(style = "print")

ggplot(
    data = data.frame(sim_moran),
    aes(x = sim_moran)
  ) +
  geom_histogram(
    bins = 30, 
    color = "#FFFCF9", 
    fill = "#1F363D",
    alpha = .8
  ) +
  # Add mean line
  geom_vline(
    xintercept = sim_mean, 
    color = "salmon", 
    linetype = "dashed", 
    linewidth = 1
  ) +
  # Add line annotations
  annotate(
    "text", 
    x = .035, 
    y = 100, 
    label = paste("Mean value =", round(sim_mean, 3)),
    color = "salmon",
    size = 3
  ) +
  labs(
    title = "Simulated Moran's I Statistic",
    subtitle= "(Based on Monte-carlo Simulation of 1000 trials)",
    x = "Moran's I Statistic",
    y = "Frequency"
  ) +
  theme(
    panel.grid.major = element_blank()
  )

15.2 Geary’s C test

Both Moran’s I and Geary’s C are measures of spatial autocorrelation. However, Geary’s C calculation is a simpler calculation, taking the ratio of the sum of squared differences between neighboring values over the total variance. Their result statistics are also inversely related:

  • C value close to 1 indicates no spatial autocorrelation
  • C value nearer to 0 indicates positive spatial correlation
  • C value nearer to 2 indicates negative spatial correlation

The code chunk below performs Geary’s C test for spatial autocorrelation by using geary.test() of spdep

code block 
geary.test(hunan$GDPPC, listw = rswm_q)

    Geary C test under randomisation

data:  hunan$GDPPC 
weights: rswm_q 

Geary C statistic standard deviate = 3.6108, p-value = 0.0001526
alternative hypothesis: Expectation greater than statistic
sample estimates:
Geary C statistic       Expectation          Variance 
        0.6907223         1.0000000         0.0073364

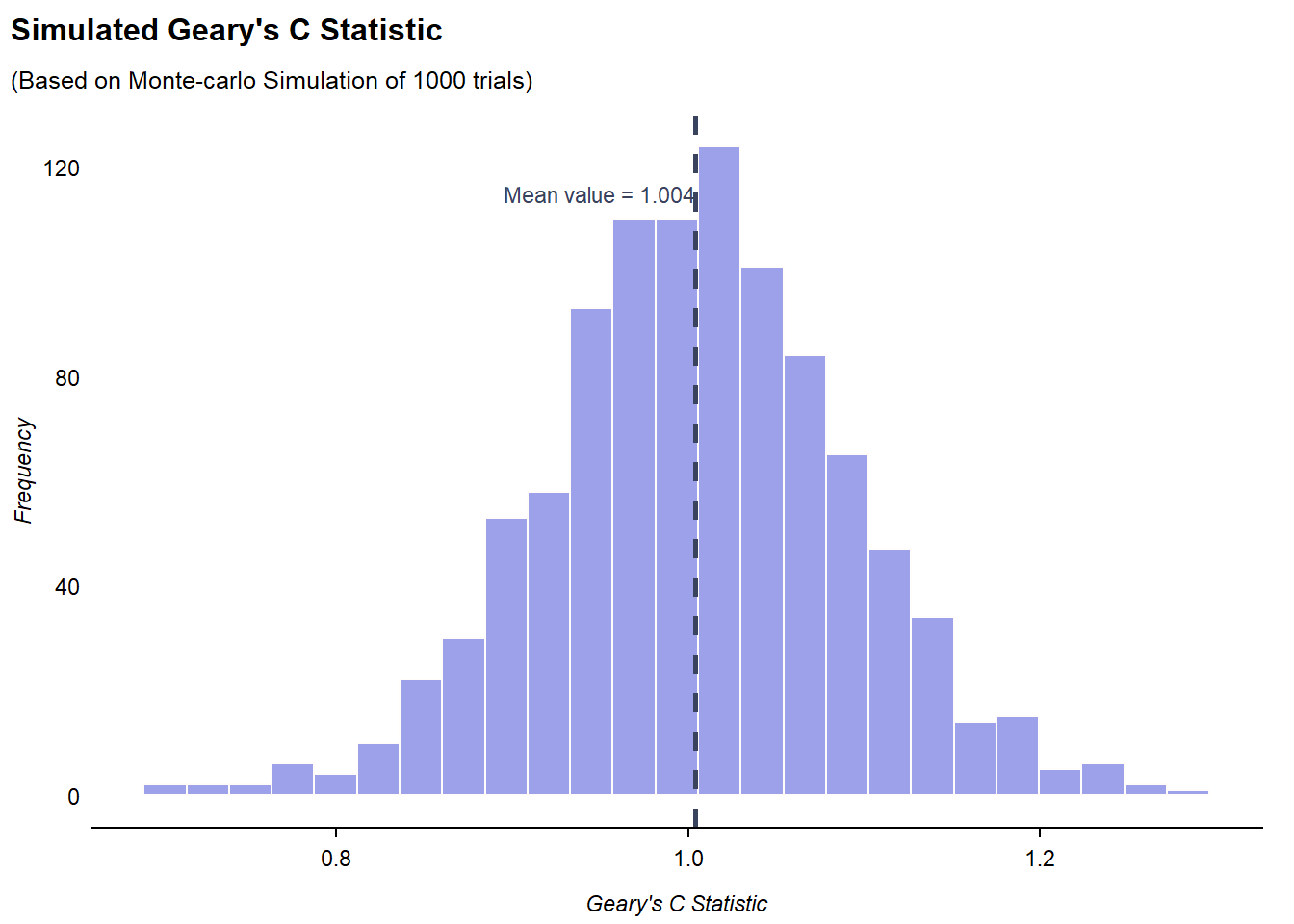
From the test results, p-value is < 0.05, so we reject \(H_0\) and conclude that the variable is not randomly distributed among the spatial features in the study area. The expected value under spatial randomness (1.0000000) is greater than the observed Geary C statistic (0.6907223), suggesting a spatial pattern of dissimilarity, where dissimilar values are clustered together.

The code chunk below performs a Monte Carlo simulation of n= 1000 trials for Geary’s C statistic by using geary.test():

set.seed(1234)
gperm <- geary.mc(hunan$GDPPC, 
                  listw = rswm_q, 
                  nsim = 999)
gperm

    Monte-Carlo simulation of Geary C

data:  hunan$GDPPC 
weights: rswm_q 
number of simulations + 1: 1000 

statistic = 0.69072, observed rank = 1, p-value = 0.001
alternative hypothesis: greater

From the test results, p-value is < 0.05, so we reject \(H_0\) and conclude that the variable is not randomly distributed among the spatial features in the study area. The alternative hypothesis is stated as “greater”, suggesting that the observed Geary C statistic is larger than expected under the assumption of spatial randomness, indicating a tendency for dissimilar values to be close to each other.

15.2.1 Visualising the results of Monte Carlo Geary C’s Test

code block 
# Extract result
sim_geary <- gperm$res
# Calculate mean result
sim_g_mean <- mean(sim_geary)

set_urbn_defaults(style = "print")

ggplot(
    data = data.frame(sim_geary),
    aes(x = sim_geary)
  ) +
  geom_histogram(
    bins = 25, 
    color = "#FFFCF9", 
    fill = "#858AE3",
    alpha = .8
  ) +
  # Add mean line
  geom_vline(
    xintercept = sim_g_mean, 
    color = "#3A435E", 
    linetype = "dashed", 
    linewidth = 1
  ) +
  # Add line annotations
  annotate(
    "text", 
    x = .95, 
    y = 115, 
    label = paste("Mean value =", round(sim_g_mean, 3)),
    color = "#3A435E",
    size = 3
  ) +
  labs(
    title = "Simulated Geary's C Statistic",
    subtitle= "(Based on Monte-carlo Simulation of 1000 trials)",
    x = "Geary's C Statistic",
    y = "Frequency"
  ) +
  theme(
    panel.grid.major = element_blank()
  )

15.3 Statistical results as correlograms

In the code chunk below, sp.correlogram() is used to compute a 6-lag spatial correlogram of GDPPC using global spatial autocorrelation Moran’s I (method = "I"):

MI_corr <- sp.correlogram(wm_q, 
                          hunan$GDPPC, 
                          order = 6, 
                        # Use Moran's I Statistic
                          method = "I", 
                          style = "W")
plot(MI_corr)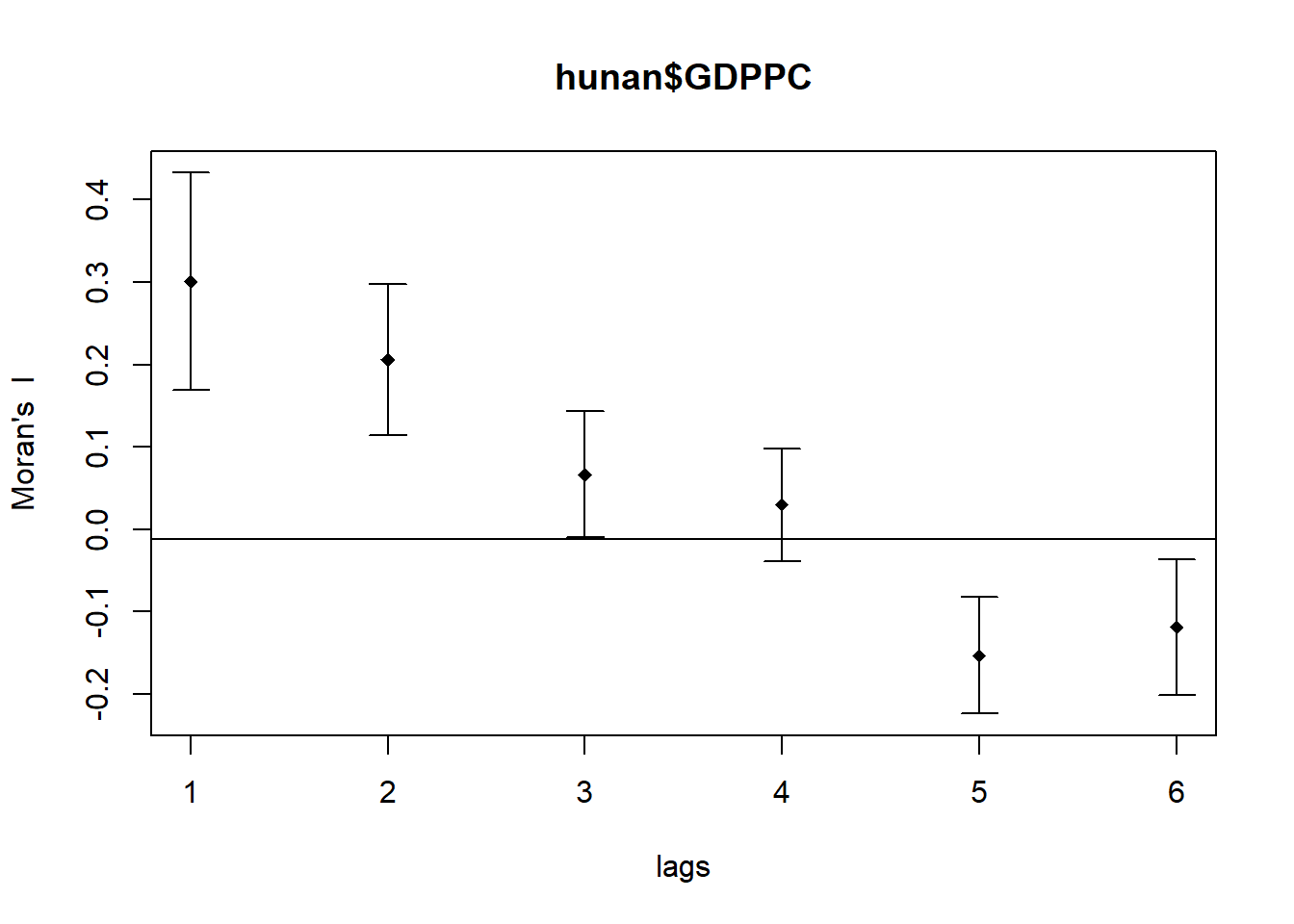

Plotting the output may not provide a complete interpretation, because not all autocorrelation values are statistically significant. Hence, it is important for us to examine the full analysis report by printing out the analysis results:

code block 
print(MI_corr)
Spatial correlogram for hunan$GDPPC 
method: Moran's I
         estimate expectation   variance standard deviate Pr(I) two sided    
1 (88)  0.3007500  -0.0114943  0.0043484           4.7351       2.189e-06 ***
2 (88)  0.2060084  -0.0114943  0.0020962           4.7505       2.029e-06 ***
3 (88)  0.0668273  -0.0114943  0.0014602           2.0496        0.040400 *  
4 (88)  0.0299470  -0.0114943  0.0011717           1.2107        0.226015    
5 (88) -0.1530471  -0.0114943  0.0012440          -4.0134       5.984e-05 ***
6 (88) -0.1187070  -0.0114943  0.0016791          -2.6164        0.008886 ** 
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

The results table has multiple columns. Each row corresponds to a specific lag distance.

  • Estimate: The observed Moran’s I statistic at each lag distance.
  • Expectation: The expected Moran’s I under the assumption of spatial randomness.
  • Variance: The variance of the Moran’s I statistic.
  • Standard Deviate: The standard deviate of the observed Moran’s I, indicating how many standard deviations the observed value is from the expected value under spatial randomness.
  • Pr(I): The p-value associated with the observed Moran’s I.
  • Two-sided: Significance codes indicating the level of significance. Smaller p-values correspond to more asterisk, indicating significance.

method = "C" uses Geary’s C Statistic instead:

GC_corr <- sp.correlogram(wm_q, 
                          hunan$GDPPC, 
                          order = 6, 
                          method  ="C", 
                          style = "W")
plot(GC_corr)

code block 
print(GC_corr)
Spatial correlogram for hunan$GDPPC 
method: Geary's C
        estimate expectation  variance standard deviate Pr(I) two sided    
1 (88) 0.6907223   1.0000000 0.0073364          -3.6108       0.0003052 ***
2 (88) 0.7630197   1.0000000 0.0049126          -3.3811       0.0007220 ***
3 (88) 0.9397299   1.0000000 0.0049005          -0.8610       0.3892612    
4 (88) 1.0098462   1.0000000 0.0039631           0.1564       0.8757128    
5 (88) 1.2008204   1.0000000 0.0035568           3.3673       0.0007592 ***
6 (88) 1.0773386   1.0000000 0.0058042           1.0151       0.3100407    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1